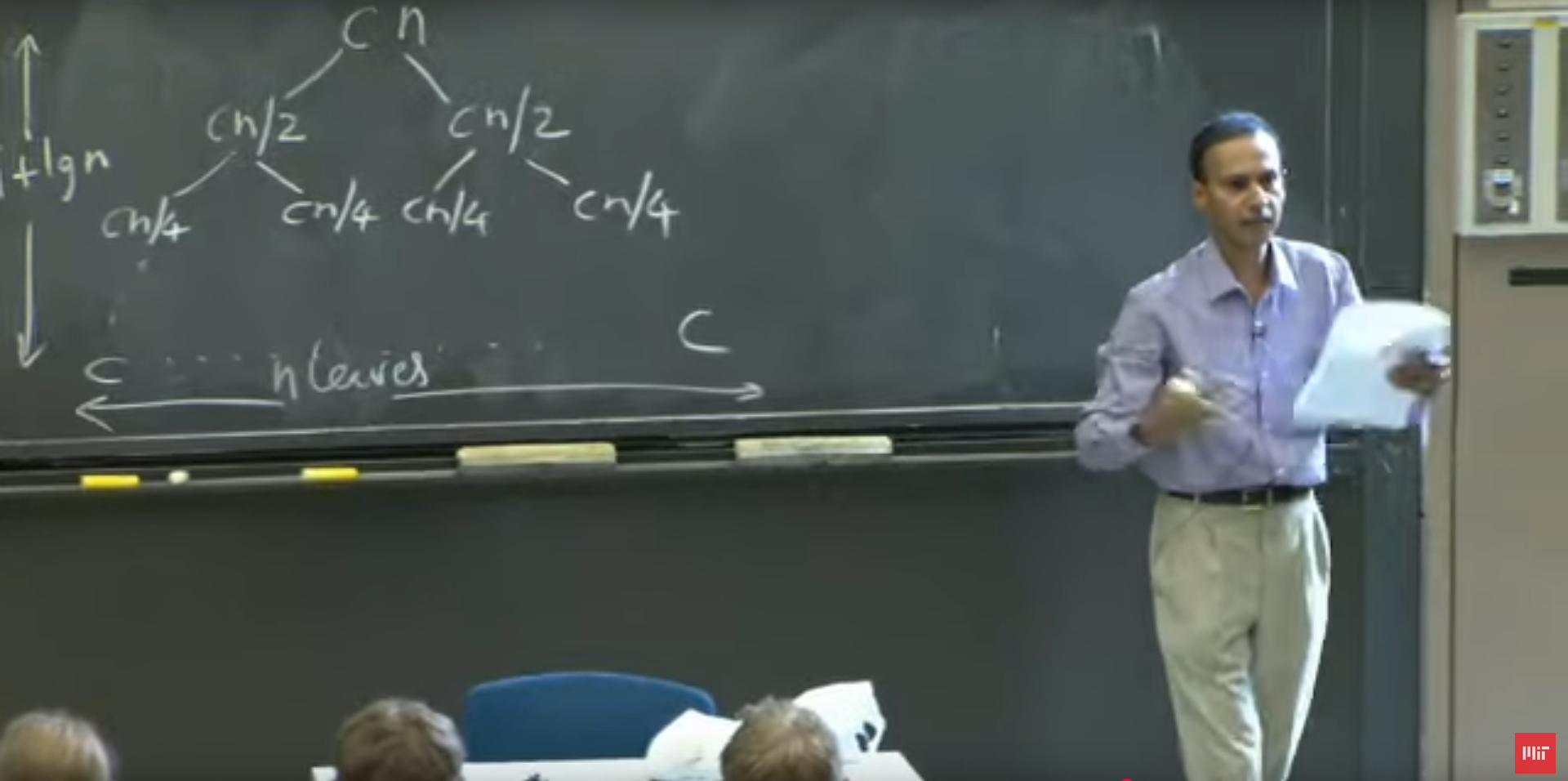MIT 6.006 Lecture 3: Merge Sort Review
Introduction
Merge sort is a recursive sorting algorithm. It has a time complexity of:
\[\Theta(n \log n)\]Its space complexity, as I recall, is proportional to (n). I am not certain whether the instructor explicitly stated this, but the creation of a copy of the original array to be sorted incurs additional space cost.
Time Complexity
The time complexity was demonstrated through a picture proof.
Recursion Tree
At each level of the recursion tree, the cost is:
\[c \cdot n\]This is split into two sub-problems:
\[\frac{c \cdot n}{2} \quad \text{and} \quad \frac{c \cdot n}{2}\]These are further divided, yielding four sub-problems of size:
\[\frac{c \cdot n}{4}\]The halving process continues, doubling the number of sub-problems at each level. Eventually, the problem is divided into $n$ units, each of cost:
\[c\]Recursion Tree Height
The height of the recursion tree was defined as:
\[1 + \log n\]I have yet to fully grasp the derivation behind this relationship.
Notes
This is an incomplete review of Lecture 3. I will update it as I continue refining my understanding of merge sort and its formal complexity analysis.